About the workshop
This workshop is organized by the Kavli Institute of Theoretical Sciences (KITS) of the University of Chinese Academy of Sciences and the Institute of Physics of the Chinese Academy of Sciences. It aims to provide i) a timely overview of the exploding field of AI for science with an emphasis on applications to the theoretical sciences; ii) a venue for researchers in AI for science to present and exchange ideas, and to identify future directions of disruptive research; and iii) an introduction for physicists to the plethora of cutting-edge ML techniques in the field of AI for science.
The topics of the workshop include:
- AI for differential equations
- Physical laws are often expressed in terms of partial differential equations (PDEs), such as Maxwell’s equations in electrodynamics, the Navier-Stokes equations in fluid dynamics, and Schrodinger’s equation in quantum mechanics. Neural networks and neural operators provide a novel paradigm to solve such PDEs by exploiting the universal representational nature of deep neural networks in either a data-driven or a self-supervised manner. Their increased performance opens the door to previously infeasibly high resolutions and amortizes the often inhibitive computational cost of large-scale PDE solvers.
- AI for theoretical high energy physics
- Machine learning provides powerful tools to tackle a wide variety of problems in theoretical high-energy physics. For example, reinforcement learning techniques can be applied successfully in the numerical conformal bootstrap program; the search for a string vacuum that describes Nature, which effectively is a computational algebraic geometry question, may be rendered surmountable; and there exists a correspondence between neural networks and field theories which potentially opens the door to a non-perturbative definition of QFTs in the continuum. What’s more, intuition, ideas, and concepts from theoretical physics have proved, time and again, to facilitate and drive novel directions of research in machine learning, such as in the blossoming field of energy-based models.
- AI for quantum mechanics and quantum chemistry
- Open quantum systems are described by a density matrix whose dynamics can often be described by a master equation. As the (complex) dimension of the density matrix scales as N^k, where N is the dimension of the Hilbert space and k the number of subsystems, the time evolution of systems with many subsystems and/or (infinitely) large Hilbert spaces is exceedingly hard. Deep generative neural networks allow one to succinctly represent the density matrix, thus reducing the computational cost of modeling their temporal evolution. Similar techniques can be applied to continuous many-body wave functions in quantum chemistry.
- AI for lattice field theory
- Lattice field theories (on a finite lattice) are defined in terms of high-dimensional probability distributions. To compute physical observables, lattice field theorists need to be able to sample reliably and efficiently from said distributions. Traditionally, Markov Chain Monte Carlo methods are brought to bear for this task, but these are known to suffer from critical slowing down – the phenomenon that consecutively generated samples are increasingly correlated – when trying to probe a critical point or the continuum limit. Several machine learning models, including real non-volume preserving flows and continuous flows based on neural ordinary differential equations, that deal gracefully with probability distributions and admit convenient sampling provide compelling alternatives and are actively investigated.
- AI for inverse design in material science, biophysics, and engineering
- Inverse design aims to answer the question which design, among all possible designs, realizes a particular desired target property. It finds applications in many scientific and engineering fields, e.g., in material science it can be deployed for the design of materials for batteries or solar cells with improved performance and in biophysics it can be leveraged to engineer biomolecules (e.g., proteins) with specific functions and properties. At heart it is an optimization problem that greatly benefits from machine learning methodologies, be it via the use of physics-informed surrogate models, invertible deep learning models, or generative AI models.

Time and venue
The workshop will take place at Room M234 in Institute of Physics, Beijing from November 11 (registration day) till November 15, 2024.
Confirmed Invited speakers
- Fanglin Bao (Westlake University): Are there physical limits on machine learning? Slides
- Aurélien Decelle (Universidad Complutense Madrid): How phase transitions shape the learning of complex data in the Restricted Boltzmann Machine
- Dong-Ling Deng (Tsinghua University): Quantum adversarial machine learning: from theory to experiment
- Bin Dong (Peking University): AI for Mathematics:from Digitization to Intelligentization
- Youngjoon Hong (KAIST): AI for Scientific Computing: Theory and Applications Slides
- Gerhard Jung (Université Grenoble Alpes): Can Generative AI Models Efficiently Sample Deeply Supercooled Liquids? Slides
- Miao Liu (IoP, CAS): A high-accuracy out-of-the-box universal AI force field for arbitrary inorganic materials Slides
- Jannes Nys (École Polytechnique Fédérale de Lausanne): Machine learning fermionic matter: strongly correlated systems in and out of equilibrium Slides
- Weiluo Ren (ByteDance Research): Recent progress in neural network based quantum Monte Carlo Slides
- Rak-Kyeong Seong (Ulsan National Institute of Science and Technology): Machine Learning the Geometry of Quantum Fields and Strings
- Tailin Wu (Westlake University): Compositional inverse design and closed-loop control of physical systems via diffusion generative models
- Han Wang (Institute of Applied Physics and Computational Mathematics): Deep learning variational free energy for atomic systems
- Yong Xu (Tsinghua University): Deep learning density functional theory and beyond
- Marius Zeinhofer ((Freiburg University): First Optimize, Then Discretize for Scientific Machine Learning Slides
- Pan Zhang (ITP, CAS): Decoding quantum error-correcting codes using generative models
- Yi Zhang (Peking University): Machine Learning for Quantum Materials, Models, and Algorithms Slides
- Kai Zhou (CUHK-SZ): Extreme QCD matter Exploration Meets Machine Learning Slides
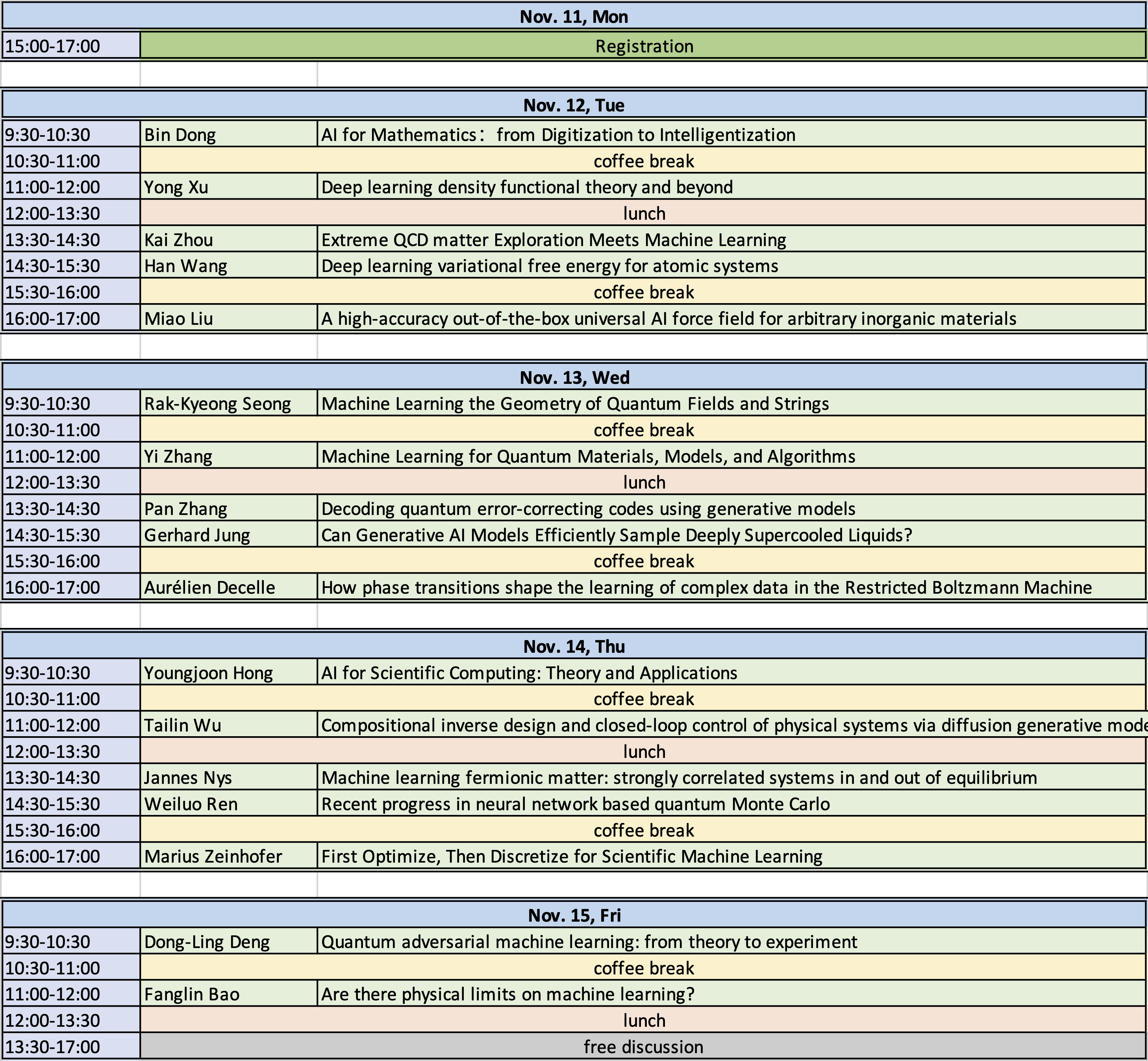
Program
Organizers
Wolfger Peelaers (HPE labs)
Lei Wang (Institute of Physics, Chinese Academy of Sciences)
Long Zhang (Kavli ITS, University of Chinese Academy of Sciences)
Xinan Zhou (Kavli ITS, University of Chinese Academy of Sciences)
Contact
Please email any questions you may have to the organizers: xinan.zhou@ucas.ac.cn
